4128. Королевства

Несколько королевств столкнулись с серьезными финансовыми трудностями. В течение многих лет они тайно занимали все больше и больше денег друг у друга. Теперь, когда разоблачены их обязательства, крах неизбежен ...

Имеются n королевств. Для каждой пары королевств (A, B) количество золота, которое королевство A обязано вернуть королевству B, выражается целым числом d_AB (мы предполагаем, что d_BA = -d_AB). Если королевство имеет отрицательное сальдо (должно платить больше, чем может получить), оно может обанкротиться. Банкротство удаляет все обязательства, как положительные, так и отрицательные, как если бы королевство перестало существовать. Затем следующее королевство может обанкротиться и так далее, пока все остальные королевства не станут финансово стабильными.

В зависимости от того, кто падает первым, могут возникнуть разные сценарии. В частности, иногда может остаться только одно королевство. Определите для каждого королевства, сможет ли оно стать единственным выжившим.

Вход. Первая строка содержит количество тестов t. Описания тестов приведены ниже:

Описание каждого теста начинается со строки, содержащей количество королевств n (1 ≤ n ≤ 20). Затем следуют n строк, каждая из которых содержит n чисел. j-ое число в i-ой строке – это количество d_ij золотых монет, которое i-ое королевство должно вернуть j-ому. Можете считать, что d_ii = 0 и d_ij = -d_ji для каждого 1 ≤ i, j ≤ n. Также |d_ij| ≤ 10⁶ для всех возможных i, j.

Выход. Для каждого теста выведите одну строку, содержащую индексы королевств, которые могут стать единственными выжившими, в порядке возрастания. Если таких королевств нет, выведите одно число 0.

Пример входа	Пример выхода
1 3 0 -3 1 3 0 -2 -1 2 0	1 3

РЕШЕНИЕ

перебор - маски

Анализ алгоритма

Для каждого j-го королевства определим sum[j] как общую сумму долга золота (sum[j] положительно если королевство имеет положительное сальдо и отрицательно иначе). Таким образом если sum[j] < 0, то j-ое королевство может обанкротиться. Значение sum[j] может быть найдено как сумма чисел j-го столбца входной матрицы.

Совершим полный перебор с возвратом процесса банкротства. Пусть mask представляет собой маску множества текущих необанкротившихся королевств. Перебираем в ней единичные биты (присутствующие королевства). Если текущее i-ое королевство может оказаться банкротом (sum[i] < 0), то удаляем его из множества, пересчитываем массив sum. Далее решаем задачу для множества mask – 2ⁱ.

Установим used[mask] = 1, если в процессе банкротств может оказаться в живых множество королевств, описываемых маской mask. Тогда i-ое королевство может оказаться единственно выжившим, если used[1 << i] будет установлено в 1.

Пример

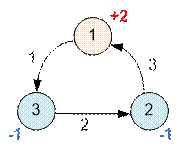
Первый обанкротиться сначала не может.

Если сначала обанкротится 2, то далее обанкротится 1. Выживет 3.

Если сначала обанкротится 3, то далее обанкротится 2. Выживет 1.

Реализация алгоритма

Массив d хранит входную матрицу. Массив sum хранит суммы долга для подмножеств королевств. used[mask] = 1, если в процессе банкротств может оказаться в живых множество королевств, описываемых маской mask.

#define MAX 20

int d[MAX][MAX], sum[MAX];

bool used[1 << MAX];

Перебор вариантов – поиск в глубину.

void dfs(int mask)

{

Подмножество королевств, описываемое mask, достигнуто.

used[mask] = true;

Перебираем королевства из множества mask. Если некоторое i-ое королевство имеет отрицательный баланс, то моделируем его банкротство (если множество mask / {i} ранее еще не встречалось).

for (int i = 0; i < n; i++)

if ((mask & (1 << i)) && sum[i] < 0 && !used[mask - (1 << i)])

{

Пересчитываем массив sum в результате удаления королевства i.

for (int j = 0; j < n; j++)

if (mask & (1 << j))

sum[j] -= d[i][j];

Продолжаем процесс банкротства множества королевств mask / {i}.

dfs(mask - (1 << i));

Мы реализуем перебор с возвратом. Возвращаем во множество i-ое королевство.

for (int j = 0; j < n; j++)

if (mask & (1 << j))

sum[j] += d[i][j];

}

}

Основная часть программы.

scanf("%d", &tests);

while (tests--)

{

Читаем входную матрицу.

scanf("%d", &n);

for (i = 0; i < n; i++)

for (j = 0; j < n; j++)

scanf("%d", &d[i][j]);

Инициализируем массивы used и sum.

for (i = 0; i < (1 << n); i++) used[i] = false;

for (i = 0; i < n; i++) sum[i] = 0;

Для каждого j-го королевства вычисляем сумму долга золота sum[j].

for (i = 0; i < n; i++)

for (j = 0; j < n; j++)

sum[j] += d[i][j];

Начинаем перебор со множества, содержащего все королевства (mask = 2ⁿ – 1).

dfs((1 << n) - 1);

Если можно достичь множества, состоящего из единственого королевства – то это королевство может оказаться единственно выжившим. Выводим его номер (нумерация королевств в задаче производится с 1).

bool flag = false;

for (int i = 0; i < n; i++)

if (used[1 << i])

{

printf("%d ", i + 1);

flag = true;

}

if (!flag) printf("0");

printf("\n");

}